Generate Aes 256 Key Python

Pycrypto is a python module that provides cryptographic services. The full form of Pycrypto is Python Cryptography Toolkit.Pycrypto module is a collection of both secure hash functions such as RIPEMD160, SHA256, and various encryption algorithms such as AES, DES, RSA, ElGamal, etc. AES is very fast and reliable, and it is the de facto standard for symmetric encryption. We use AES in a mode of operation in order to encrypt. The solutions above suggest using CBC, which is one example. Another is called CTR, and it’s somewhat easier to use: # AES supports multiple key sizes: 16 (AES128), 24 (AES192), or 32 (AES256). # pair (iv, ciphtertext). 'iv' stands for initialization vector. Need to encrypt some text with a password or private key in Python? You came to the right place. AES-256 is a solid symmetric cipher that is commonly used to encrypt data for oneself. AES (Advanced Encryption Standard) is a symmetric block cipher standardized by NIST. It has a fixed data block size of 16 bytes. Its keys can be 128, 192, or 256 bits long. AES is very fast and secure, and it is the de facto standard for symmetric encryption. The recipient can obtain the original message using the same key and the. Python Create Aes Key Generate Aes Key Openssl Mar 12, 2020 Generating AES keys and password Use the OpenSSL command-line tool, which is included with InfoSphere® MDM, to generate AES 128-, 192-, or 256-bit keys. The madpwd3 utility is used to create the password.

This is a continuation of my previous post. I finished the encryption portion of my Python implementation of the AES-256 algorithm, and in this post I'll cover some of the details.

AES 256 Encryption in Python

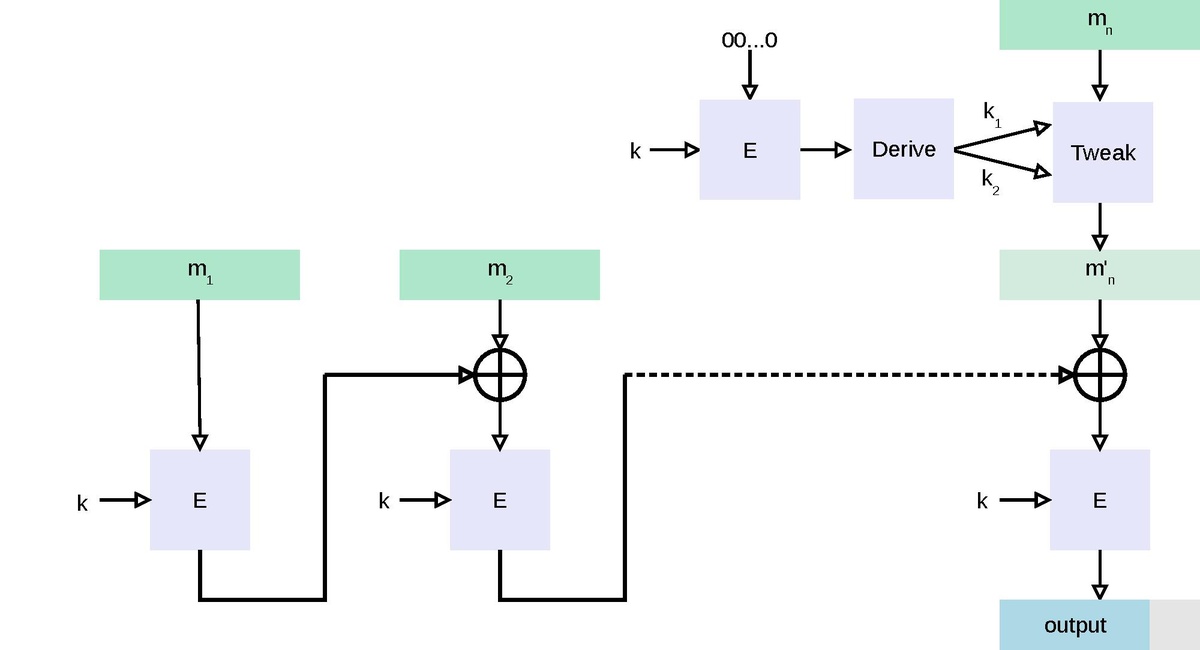
In my last post I left off after the key expansion portion of the algorithm. The next step is to carry out the encryption of the input data. First, the input data is split into a 4x4 matrix called the state matrix. The AES encryption operations work on this matrix. The first 4 bytes of the input data become the first column of the matrix, the next 4 bytes the second column, and so on. I created a function to initialize a two dimensional list with the input data to represent the state matrix, named matrix.

Next, the input data is XOR'd with the first of the round keys (round_key[0]). This operation is repeated throughout the encryption process, so I created a function to do it. (The function dumpMatrix() is a utility for printing the state matrix to aid in debugging, it is not a part of the AES process.)

AES-256 uses 14 rounds of encryption. Each round is the same except for the final round which skips over the mix columns step. Each round uses its respective round key. The loop below carries out the encryption rounds.

The first step in each round is the substitute bytes operation. This operation makes use of the same substitution table, or S-box, as the key schedule. I covered the generation of the S-box in my previous post. Each byte in the matrix is substituted in-place. The S-box operation is non-linear and helps prevent linear analysis of the algorithm among other attacks.

The next two steps, shift rows and mix columns provide diffusion for the AES algorithm, i.e. ensuring that small changes in the plaintext result in large differences in the ciphertext. The shift rows step consists of leftward rotations of the last three rows of the state matrix. The second row is shifted one place, the third row is shifted two places, and the final row is shifted three places. I wrote a helper function to carry out the rotation of a single row, and a function called shift_rows() to operate on the state matrix.

The mix columns operation involves multiplying each column of the state matrix by a constant matrix defined by the AES specification. The multiplication is done in the AES finite field defined by the AES irreducible polynomial, P = x^8 + x^4 +x^3 + x + 1. I covered finite field multiplication and addition in my previous post, but in short, the result of the multiplication is reduced modulo P. Addition is carried out in the prime field GF(2), i.e. modulo 2, the equivalent of the XOR operation. To perform the mix columns operation, I created the following function.

This function calls mmult to carry out the matrix multiplication. The multiplication operations in mmult use a helper function for multiplication in GF(2^8). The constant values in the mmult function corresponds to those defined in the constant matrix in the AES specification. In places that the constant is 1, the multiplication operation is skipped.

The function gf2mult is an algorithmic way of multiplying a byte in GF(2^8) using the shift-and-add method, operating on bit vector representations of members of the field. I covered this in more detail in my previous post. Keep in mind, the XOR operation is equivalent to addition (and subtraction) in GF(2^8). The highest bit of the operand x is checked and, if set, indicates that the result of the multiplication exceeds the degree of the irreducible polynomial p and that it must be reduced. This is done by subtracting away the bit vector representation of p via XOR.

The mix columns operation is not included in the final round of encryption as a design choice by in the AES specification because it does not enhance the security of the algorithm.

The final step in the encryption round is XOR'ing the state matrix with the corresponding round key. This operation uses the same add_round_key function described above. Lastly, the ciphertext is reconstructed from the state matrix.

Testing and Verification

Running the script results in the following ciphertext (given the key and input data below):

As a quick validity check, I verified the output of my implementation against the python PyCrypto library's AES-256 ECB implementation.

Running this script results in the expected output.

Summary

As I've mentioned in previous posts, I've found it very helpful to write code in Python because it is an easy to write/read/run/debug language and it gives me a good baseline to work from in Verilog. The next post will cover the encryption portion of the algorithm in Verilog.

Let's illustrate the AES encryption and AES decryption concepts through working source code in Python.

The first example below will illustrate a simple password-based AES encryption (PBKDF2 + AES-CTR) without message authentication (unauthenticated encryption). The next example will add message authentication (using the AES-GCM mode), then will add password to key derivation (AES-256-GCM + Scrypt).

Simple AES-CTR Example

Let's start with simple AES-256-CTR non-authenticated encryption.

Install Python Libraries `pyaes` and `pbkdf2`

First, install the Python library pyaes that implements the AES symmetric key encryption algorithm:

Next, install the Python library pbkdf2 that implements the PBKDF2 password-to-key derivation algorithm:

Now, let's play with a simple AES encrypt / decrypt example.

Password to Key Derivation

First start by key derivation: from password to 256-bit encryption key.

Run the above code example: https://repl.it/@nakov/AES-CTR-in-Python.

The above code derives a 256-bit key using the PBKDF2 key derivation algorithm from the password s3cr3t*c0d3. It uses a random password derivation salt (128-bit). This salt should be stored in the output, together with the ciphertext, because without it the decryption key cannot be derived again and the decryption will be impossible.

The output from the above code may look like this:

The derived key consists of 64 hex digits (32 bytes), which represents a 256-bit integer number. It will be different if you run the above code several times, because a random salt is used every time. If you use the same salt, the same key will be derived.

AES Encryption (CTR Block Mode)

Next, generate a random 256-bit initial vector (IV) for the AES CTR block mode and perform the AES-256-CTR encryption:

Run the above code example: https://repl.it/@nakov/AES-encryption-in-Python.

The output from the above code may look like this:

The ciphertext consists of 38 hex digits (19 bytes, 152 bits). This is the size of the input data, the message Text for encryption.

Generate 256 Bit Aes Key Python

Note that after AES-CTR encryption the initial vector (IV) should be stored along with the ciphertext, because without it, the decryption will be impossible. The IV should be randomly generated for each AES encryption (not hard-coded) for higher security.

Note also that if you encrypt the same plaintext with the same encryption key several times, the output will be different every time, due to the randomness in the IV. This is intended behavior and it increases the security, e.g. resistance to dictionary attacks.

AES Decryption (CTR Block Mode)

Now let's see how to decrypt a ciphertext using the AES-CTR-256 algorithm. The input consists of ciphertext + encryption key + the IV for the CTR counter. The output is the original plaintext. The code is pretty simple:

Run the above code example: https://repl.it/@nakov/AES-decryption-in-Python.

The output of the above should be like this:

Note that the aes object should be initialized again, because the CTR cipher block mode algorithm keeps an internal state that changes over the time.

Note also that the above code cannot detect wrong key, wrong ciphertext or wrong IV. If you use an incorrect key to decrypt the ciphertext, you will get a wrong unreadable text. This is clearly visible by the code below:

Run the above code example: https://repl.it/@nakov/AES-decryption-wrong-key-in-Python.

The output of the above incorrect decryption attempt might be like this:

Now it is your time to play with the above code example. Try to to encrypt and decrypt different messages, to change the input message, the key size, to hard-code the IV, the key and other parameters, switch to CBC mode, and see how the results change. Enjoy learning by playing.

AES-256-GCM Example

Now, let's give a full example how to use the AES-256-GCM symmetric encryption construction. We shall use a different Python library for AES, called pycryptodome, which supports the the AES-256-GCM construction:

Next, let's play with the below AES-GCM example in Python, which generates a random encryption key (secret key) and uses it to encrypt a text message, then decrypts it back to the original plaintext message:

Run the above code example: https://repl.it/@nakov/AES-256-GCM-in-Python.

The AES-GCM encryption takes as input a message + encryption key and produces as output a set of values: { ciphertext + nonce + authTag }.

The ciphertext is the encrypted message.
The nonce is the randomly generated initial vector (IV) for the GCM construction.
The authTag is the message authentication code (MAC) calculated during the encryption.

The encryption key size generated in the above code is 256 bits (32 bytes) and it configures the AES-GCM cipher as AES-256-GCM. If we change the key size to 128 bits or 192 bits, we shall use AES-128-GCM or AES-192-GCM respectively.

The output from the above code looks like this:

It is visible that the encryption key above is 256 bits (64 hex digits), the ciphertext has the same length as the input message (43 bytes), the IV is 128 bits (32 hex digits) and the authentication tag is 128 bits (32 hex digits). If we change something before the decryption (e.g. the ciphertext of the IV), we will get and exception, because the message integrity will be broken: